题目连接:Gold Miner
Gold Miner
这题要求至多进行 50 次操作,要能够将 $n\times n$ 的网格除对角线和对角线下发一条线全部涂满。每次可以选择若干行和若干列,将它们的交点涂上色。
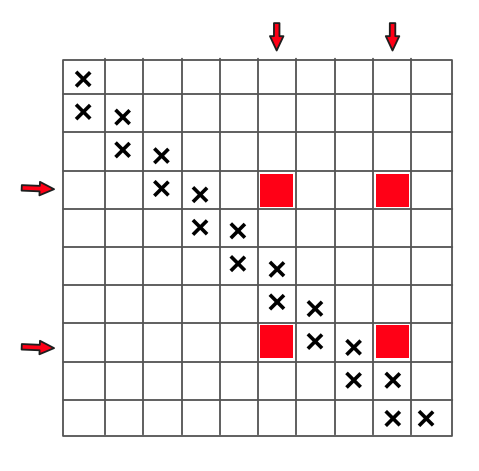
提示中说使用分治来思考。令 $T(n)$ 是 $n$ 大小的网格需要进行的操作次数(不是程序的运行时间),思考如何用 $T(\frac{n}{2})$ 来解决 $T(n)$。因为有一半,首先想到的是分割网格成 $\frac{n}{2}\times\frac{n}{2}$ 大小的子网格如下:
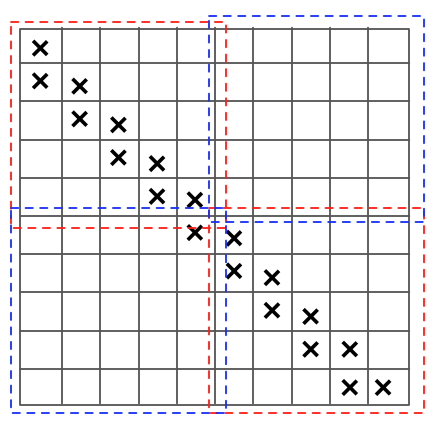
如图按左上,左下,右上,右下正好分割成四块。其中,蓝色区域的很容易上色,用 3 次操作即可全部上色。而左上和右下又是两个 $T(\frac{n}{2})$ 的子问题,故按此方法可得 $T(n)=2T(\frac{n}{2})+3$。
观察到左上和右下在横纵坐标的限制上耦合度很低,理想的情况是在左上的横纵坐标选择和右下的横纵坐标选择之间完全不影响(相互为独立的子问题)。这样我们就可以把左上中一次操作和右下中一次操作合并在一起,作为一次操作。总操作数即为 $T(n)=T(\frac{n}{2})+3$。但左下有一个不能选中的地方,这导致左上选择纵坐标 5 的时候,右下不能选中横坐标 6。为了解决这个问题,在划分子问题时必须是两个矩形的横纵坐标相交处没有禁止的点。
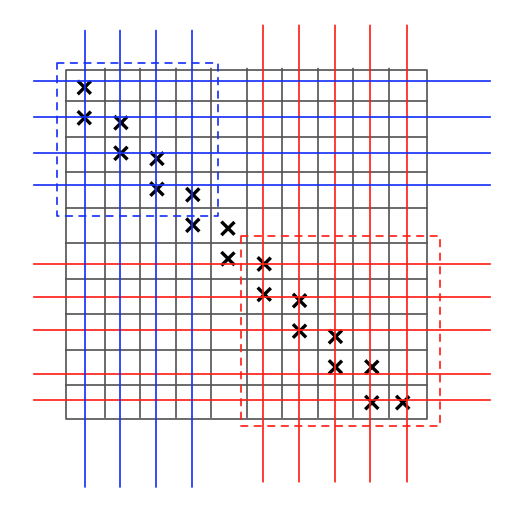
一种可行的方法是缩小左上的矩形,如此交点处都是可以的。根据题目中 “It is allowed to enter some cells multiple times!”,上下两个子矩阵的求解就成为相互独立的子问题了。此时其余部分用 4 次操作可以填满。$n=3000,\log_2 n \approx 11,4*11=44<50$
程序实现时,可以递归模拟二分过程,既可以用 vector 记录选择的 $X,Y$ 坐标,merge 时合并,也可以用全局变量记录。其中,特殊处理一下 $n=1,2,3,4$ 的情况,可以让染色数减少(如 $n=4$ 只需 3 次)。
示例代码
#include <bits/stdc++.h>
using namespace std;
#define max_n 3000
#define max_round 50
int n;
bool X[max_round + 1][max_n + 1], Y[max_round + 1][max_n + 1];
int solve(int n, int low, int round) {
/**
* n: size of matrix
* low: the index of first row in this matrix
* according to the original matrix
* round: number of round
*/
// Special case for n<=4
if (n == 1) {
return round;
} else if (n == 2) {
round += 1;
X[round][low] = Y[round][low + 1] = true;
return round;
} else if (n == 3) {
round += 1;
X[round][low] = Y[round][low + 1] = Y[round][low + 2] = true;
round += 1;
X[round][low + 1] = Y[round][low + 2] = true;
round += 1;
X[round][low + 2] = Y[round][low] = true;
return round;
} else if (n == 4) {
round += 1;
X[round][low + 2] = X[round][low + 3] = Y[round][low] = true;
round += 1;
X[round][low] = X[round][low + 3] = Y[round][low + 1] = true;
round += 1;
X[round][low] = X[round][low + 1] = Y[round][low + 2] =
Y[round][low + 3] = true;
round += 1;
X[round][low + 2] = Y[round][low + 3] = true;
return round;
}
// 4 rounds for up_right and down_left
int up_n, down_n, down_low;
up_n = (n - 1) / 2;
down_n = n - up_n - 1;
down_low = low + up_n + 1;
// round 1
round += 1;
for (int d = 0; d < down_n; ++d) X[round][down_low + d] = true;
for (int d = 0; d < up_n; ++d) Y[round][low + d] = true;
// round 2
round += 1;
for (int d = 0; d < up_n; ++d) X[round][low + d] = true;
for (int d = 0; d < down_n; ++d) Y[round][down_low + d] = true;
// round 3
round += 1;
X[round][low + up_n] = true;
for (int d = 0; d < n; ++d) {
if (d != up_n and d != up_n - 1) Y[round][low + d] = true;
}
// round 4
round += 1;
Y[round][low + up_n] = true;
for (int d = 0; d < n; ++d) {
if (d != up_n and d != up_n + 1) X[round][low + d] = true;
}
// solve up_left and down_right
int up_round = solve(up_n, low, round);
int down_round = solve(down_n, down_low, round);
return max(up_round, down_round);
}
void output_round(bool* X) {
bool is_first = true;
for (int j = 1; j <= n; ++j) {
if (X[j]) {
if (is_first) {
printf("%d", j);
is_first = false;
} else {
printf(" %d", j);
}
}
}
printf("\n");
}
int main() {
// Input
scanf("%d", &n);
// Solve by Divide & Conquer
int round = solve(n, 1, 0);
// Output
// printf("%d\n", round);
for (int i = 1; i <= round; ++i) {
output_round(X[i]);
output_round(Y[i]);
}
return 0;
}