Applications

How Data Flows on CFG? How application-specific Data Flows through the Nodes (BB) and Edges (control flows) of CFG (a program)

• may analysis: over-approximation
• must analysis: under-approximation
• input and output statses
• Transfer Function
  • forward analysis: $\text{OUT}[s]=f_s(\text{IN}[s])$
  • backward analysis: $\text{IN}[s]=f_s(\text{OUT}[s])$
• Control Flow
  • $\text{IN}[B]=\bigwedge_{P\text{ a predecessor of }B}\text{OUT}[P]$
• Key
  • Domain, Direction, May/Must, Boundary, Initialization, Transfer function, Meet

Reaching Definitions Analysis

• definition of a variable: a statement that assigns to a value
• whether the a definition d is reachable at program point p
• usage
  • detect possible undefined variables
• $\text{OUT}[B]=\text{gen}_B\cup(\text{IN}[B]-\text{kill}_B)$

Live Variables Analysis

• whether the value of variable v at program point p could be used along som path in CFG starting at p
• usage
  • register allocations
• $\text{OUT}[B]=\bigcup_{\text{S a successor of B}}\text{IN}[B]$
• $\text{IN}[B]=\text{use}_B\cup(\text{OUT}[B]-\text{def}_B)$

Available Expressions Analysis

• whether an expression must be constant at a point
• x op y is available if
  • all paths from the entry to p must pass through the evalution of x op y
  • after the last evaluation of x op y, there is no redefinition of x or y
• must-analysis

Constant Propagation

• Given a variable $x$ at program point $p$, determine whether $x$ is guaranteed to hold a constant value at $p$
• $\text{OUT}[B]=(x,v)$
• nondistributivity

Lattice

• Partial Order: poset $(P,\subseteq),\subseteq$ is binary relation that defines a partial ordering over $P$, $\subseteq$ has the following properties:
  • reflexity: $\forall x\in P,x\subseteq x$
  • antisymmetry: $\forall x,y\in P,x\subseteq y\wedge y\subseteq x\Rightarrow x = y$
  • transtivity: $\forall x,y,z\in P,x\subseteq y\wedge y\subseteq z\Rightarrow x\subseteq z$
• upper bound $u$: $\forall x\in S, x\subseteq u, S\subseteq P$
• lower bound $1$: $\forall x\in S, 1\subseteq x$
• least upper bound(lub or join) $\cup S\in P$: $\forall u, \cup S\subseteq u$
  • two elements: $a\cup b$
• greatest lower bound(glb or meet) $\cap S$: $\forall 1, 1\subseteq\cap S$
  • two elements: $a\cap b$
  • lub and glb is unique
• lattice: $\forall a,b\exists a\cup b,a\cap b$
• semilattice: $\forall a,b\in P$
  • only $a\cup b$ exists, $(P,\subseteq)$ is called a join semilattice
  • only $a\cap b$ exists, $(P, \subseteq)$ is called a meet semilattice
• complete lattice: $\forall S\subseteq P,\exists\cup S,\cap S$
  • greatest element $\top=\cup P$
  • least element $\perp=\cap P$
• Every finite lattice is a complete lattice
• Product Lattice: $L_i=(P_i,\subseteq_i),L^n=(P,\subseteq)$
  • $P=P_1\times\cdots\times P_n$
  • $(x_1,\cdots, x_n)\subseteq (y_1,\cdots, y_n)\iff (x_1\subseteq y_1)\wedge\cdots\wedge (x_n\subseteq y_n)$
• A product lattice is a lattice
• if a product lattice $L$ is a product of complete lattices, then $L$ is also complete
• monotonicity: $f:L\rightarrow L,\forall x,y\in L,x\subseteq y\Rightarrow f(x)\subseteq f(y)$
• fixed-point theorem: if $f:L\rightarrow L$ is monotonic and $L$ is finite, then the least fixed point of $f$ can be found by iterating $f^k(\perp)$ until a fixed point is reached, greatest fixed point of $f$ can be found by iterating $f^k(\top)$
• height of a lattice $h$: the length of the longest path from Top to Bottom in the lattice
• distributed $F$: $F(x\cup y)=F(x)\cup F(y)$

Foundation

• Iterative Algorithm (IN/OUT equation system)

  • Input: CFG (kill and gen computed for each basic block B)
  • Output IN[B] and OUT[B] for each basic block B
  • Algorithm

OUT[entry] = {}
for (each basic block B-entry)
	OUT[B] = {}
while (changes to any OUT occur)
	for (each basic block B-entry){
		IN[B] = union_{P a predecessor of B} OUT[P]
		OUT[B] = gen_B union (IN[B] - kill_B)
	}

• CFG with $k$ nodes: $X_i=(\text{OUT}[n_1],\dots,\text{OUT}[n_k])_i\in V^k,F:V^k\rightarrow V^k$
  • $X_{i+1}=F(X_i)$
  • fixed point $X_i=X_{i+1}$
• Data Flow Analysis Framework $(D,L,F)$
  • $D$: a direction of data flow
  • $L$: a lattice including domain of the values $V$ and a meet or join operator
  • $F$: a family of transfer functions from $V$ to $V$
• Lattice height $h$, number of nodes $k$, at most $i=hk$ iterations
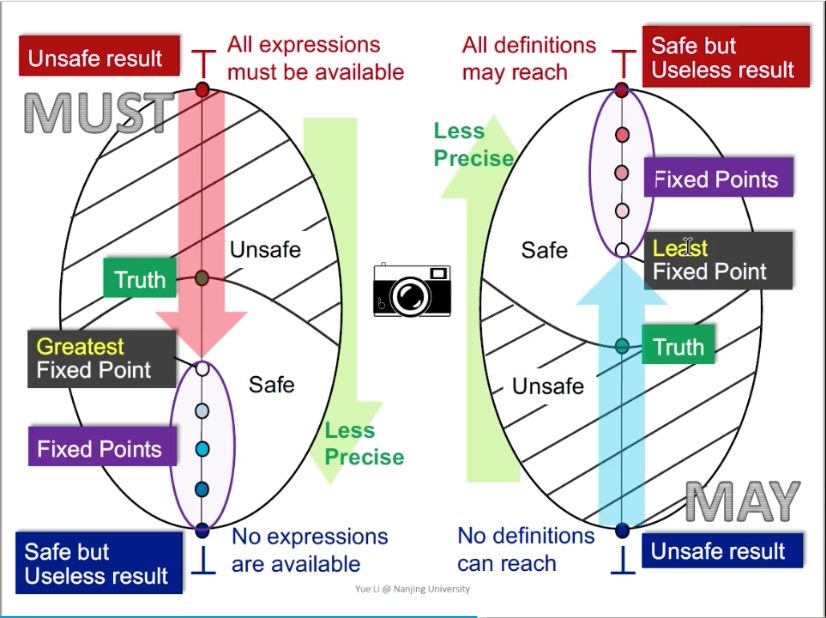
• may analysis
  • bottom $\perp$: unsafe = no definitions can reach
  • top $\top$: safe but useless result = all definitions may reach
  • truth
  • least fixed point
• must analysis
  • top $\top$: unsafe - all expressions must be available
  • bottom $\perp$: safe but useless result - no expressions are availble
  • greatest fixed point

• MOP(Meet Over all Paths): $\text{MOP}[s_i]=\cup/\cap_{\text{A path P from Entry to }S_i} F_P(\text{OUT}[\text{Entry}])$
  • $F(x)\cup F(y)\subseteq F(x\cup y)$
  • MOP $\subseteq$ Ours
  • distributive then $=$ (Bit-vecotr or Gen/Kill problem)
• Worklist Algorithm: add successors of changed B to Worklist