4. Linear Programs

Definition

Linear Programming Problem: the problem of either minimizing or maximizing a linear function subject to a finite set of linear constraints
- feasible solution, feasible area, objective function, objective value, optimal solution, optimal objective value
unbounded: have a infinite objective value
infeasible: no feasible value
Equivalent: for each feasible solution $\overline{x}$ to $L$ with objective value $z$, there is a corresponding feasible solution $\overline{x}’$ to $L’$ with objective value $z’$, and for each feasible solution $\overline{x}’$ to $L’$ with objective value $z’$, there is a corresponding feasible solution $\overline{x}$ to $L$ with objective value ́.

Standard Form

Maximize $\sum_{j=1}^nc_jx_j$
subject to $\sum_{j=1}^na_{ij}x_j\leq b_i, x_{j}\geq 0$
Converting to Stand Form
- Turn Minimize to Maximize
- $x=x_1-x_2,x_1>0,x_2>0$
- Turn equation to inequation
- Turn $\geq$ to $\leq$
$(A,b,c)$
- Maximize $c^Tx$
- subject to $Ax\leq b,x\geq 0$

Slack Form

Maximize $\sum_{j=1}^nc_jx_j$
subject to
- $x_{n+i}=\sum_{j=1}^nt_jx_j\geq0$
- $x_i\geq 0$
basic variable: Left side of equation
nonbasic variable: Right side of equation
$(N,B,A,b,c,v)$
- Maximize $c^Tx+v$
- subject to
  - $x_i=b_i-\sum_{j\in N}a_{ij}x_j,i\in B$
  - $x_i\geq 0,i\in N$

Simplex Algorithm

pivot: choose a nonbasic varible(entering variable) and a basic variable(leaving variable) and exchange their roles.
- $(N,B,A,b,c,v)\rightarrow (\hat{N},\hat{B},\hat{A},\hat{b},\hat{c},\hat{v})$
at most $\binom{n+m}{m}$ iterations, otherwise cycles
Bland’s rule: choose smallest index then must terminate

//n: number of variable
//m: number of restriction

void pivot(int l, int e) {
    // Update leaving basic variable
    b[l] /= a[l][e];
    for (int j = 1; j <= n; j++)
        if (j != e) a[l][j] /= a[l][e];
    a[l][e] = 1 / a[l][e];
    // Update other basic variable
    for (int i = 1; i <= m; i++)
        if (i != l && fabs(a[i][e]) > 0) {
            b[i] -= a[i][e] * b[l];
            for (int j = 1; j <= n; j++)
                if (j != e) a[i][j] -= a[i][e] * a[l][j];
            a[i][e] = -a[i][e] * a[l][e];
        }
    // Update entering nonbasic variable
    ans += c[e] * b[l];
    for (int j = 1; j <= n; j++)
        if (j != e) c[j] -= c[e] * a[l][j];
    c[e] = -c[e] * a[l][e];
}

double simplex() {
    while (true) {
        int enter = 0, leave = 0;
        // Select enter variable
        for (enter = 1; enter <= n; ++enter)
            if (c[enter] > eps) break;
        if (enter == n + 1) return ans;
        // Select leave variable
        double mn = INF;
        for (int i = 1; i <= m; ++i)
            if (a[i][enter] > eps && mn > b[i] / a[i][enter]) {
                mn = b[i] / a[i][enter];
                leave = i;
            }
        if (mn == INF) return INF;
        pivot(leave, enter);
    }
}

Formulating Problems

Shortest Path
- Maximize $d_t$
- subject to $d_v\leq d_u+w(u,v),d_s=0$
Maximum Flow
- Maximize $\sum_{v\in V}f_{sv}-\sum_{v\in V}f_{vs}$
- subject to $f_{uv}\leq c(u,v),\sum_{v\in V}f_{vu}=\sum_{v\in V}f_{uv},f_{uv}\geq 0$
Minimum-cost Flow
- Minimize $\sum_{(u,v)\in E}a(u,v)f_{uv}$
- subject to $f_{uv}\leq c(u,v), \sum_{v\in V}f_{vu}-\sum_{v\in V}f_{uv}=0,f_{uv}\geq 0,\sum_{v \in V}f_{sv}-\sum_{v\in V}f_{vs}=d$
Multicommodity Flow
- Minimize $0$
- subject to $\sum_{i=1}{k}f_{iuv}\leq c(u,v),\sum_{v\in V}f_{iuv}-\sum_{v\in V}f_{ivu} = 0,\sum_{v\in V}f_{is_iv}-\sum_{v\in V}f_{ivs_i}=d_i,f_{iuv}\geq 0$
vertex cover

$$\min \sum_{v\in V}x_v\newline s.t. \sum_{v\in e}x_v\geq 1,e\in E\newline x_v\in {0,1},v\in V$$

System of difference contraints
- subject to: $x_i-x_j\leq c_k$ ($m$ pairs)

Duality

Prime

$$\min c^Tx\newline s.t.\ Ax\geq b\newline x\geq 0$$

Dual

$$\max b^Ty\newline s.t.\ y^TA\leq c^T\newline y\geq 0$$

prime	dual
$\max c_1x_1+\cdots+c_nx_n$	$\min b_1y_1+\cdots+b_my_m$
$a^Tx\geq b$	$y_i\leq 0$
$a^Tx=b$	-
$a^Tx\leq b$	$y_i\geq 0$
-	$y_i=0$
$x_i\geq 0$	$a^Ty\geq c$
$x_i\leq 0$	$a^Ty\leq c$
-	$a^Ty=c$
$x_i=0$	-

Weak Duality Theorem: $\forall$ feasible primal solution $x$ and dual solution $y$

$$y^Tb\leq y^TAx\leq c^Tx$$

Strong Duality Theorem: Primal LP has finite optimal solution $x^*$ iff dual LP has finite optimal solution $y^{T}b=c^Tx^$
Complementary Slackness Condition: $\forall$ feasible primal solution $x$ and dual solution $y$, both $x$ and $y$ are optimal iff

$$\forall i:A_{i\cdot}x=b_i\vee y_i=0\newline \forall j:y^TA_{\cdot j}=c_j\vee x_j=0$$

Relaxed Complementary Slackness: $\forall$ feasible primal solution $x$ and dual solution $y$, for $\alpha,\beta\geq 1$

$$\forall i:A_{i\cdot}x\leq \alpha b_i\vee y_i=0\newline \forall j:y^TA_{\cdot j}=\frac{c_j}{\beta}\vee x_j=0\newline \Rightarrow c^Tx\leq\alpha\beta b^Ty\leq\alpha\beta\text{OPT}_{\text{IP}}$$

Fundamental theorem of linear programming: Any linear program L, given in standard form, either:
- has an optimal solution with a finite objective value
- infeasible
- unbounded

Primal-Dual Schema

The Primal-Dual Schema
- Write down an LP-relaxation and its dual
- Start with a primal infeasible solution $x$ and a dual feasible solution $y$ (usually $x=0,y=0$)
- Raise $x$ and $y$ until $x$ is feasible:
  - raise $y$ until some dual constrints gets tight $y^TA_{\cdot j}=c_j$
  - raise $x_i$ (integrally) corresponding to the tight dual constraints
- Show the complementary slackness conditions
  - $\forall i, A_{i\cdot}x\leq\alpha b_i$ or $y_i=0$
  - $\forall j,y^TA_{\cdot j}=c_j$ or $x_j=0$
  - $c^Tx\leq\alpha b^Ty\leq\alpha\text{OPT}$
Integrality Gap: $\sup_I\frac{\text{OPT}(I)}{\text{OPT}_{\text{LP}}(I)}$

Vertex Cover

Primal

$$\min \sum_{v\in V}x_v\newline s.t.\ \sum_{v\in e}x_v\geq 1,\forall e\in E\newline x_v\in{0,1},\forall v\in V$$

Dual

$$\max \sum_{e\in E}y_e\newline s.t.\ \sum_{e\owns v}y_e\leq 1,\forall v\in V\newline y_e\geq 0,\forall e\in E$$

Initially $x=0,y=0$
Raise $x$ and $y$ until $x$ is feasible
- pick an $e\in E$ and raise $y_e$ to 1, set $x_v=1$ for $v\in e$ and delete all $e\owns v$ from $E$
- Find a maximal matching and return the set of matched vertices
Integrality Gap: $2$

Facility Location

Facility location $\in\text{NPH}$
- Instance
  - $F$: Facilities
  - $C$: clients
  - $f: F\rightarrow[0,\infty)$: Facility opening costs
  - $c: F\times C\rightarrow [0,\infty)$: Facility connecting cost
- total cost: $\sum_{j\in C}c_{\phi(j),j}+\sum_{i\in I}f_i$
- Find $I\subset F$ and $\phi:C\rightarrow I$ minimize total cost
Metric Facility Location: $c_{\phi(j),j}=d_{\phi(j)j}$
- triangle inequality: $d_{i_1j_1}+d_{i_2j_1}+d_{i_2j_2}\geq d_{i_1j_2}$
Primal

$$\min \sum_{i\in F,j\in C}d_{ij}x_{ij}+\sum_{i\in F}f_iy_i\newline s.t.\ y_i-x_{ij}\geq0,\forall i\in F,j\in C\newline \sum_{i\in F}x_{ij}\geq 1,\forall j\in C\newline x_{ij},y_i\in{0,1},\forall i\in F,j\in C$$

Dual

$$\max\sum_{j\in C}\alpha_j\newline s.t.\ \alpha_j-\beta_{ij}\leq d_{ij},\forall i\in F,j\in C\newline \sum_{j\in C}\beta_{ij}\leq f_i,\forall i\in F\newline \alpha_j,\beta_{ij}\geq 0,\forall i\in F,j\in C$$

Initially $\alpha=0,\beta=0$
raise $\alpha_j$ for all client $j$ simultaneously at a uniform continous rate
- upon $\alpha_j=d_{ij}$ for a closed facility $i$: edge $(i,j)$ is paid, fix $\beta_{ij}=\alpha_j-d_{ij}$
- upon $\sum_{j\in C}\beta_{ij}=f_i$: tentatively open facility $i$; all unconnected clients $j$ with paid edge $(i,j)$ to facility $i$ are declared connected to facility $i$ and stop raising $\alpha_j$
- upon $\alpha_j=d_{ij}$ for an unconnected client $j$ and tentatively open facility $i$: client $j$ is declared connected to facility $i$ and stop raising $\alpha$
Integrality Gap: $3$

LP Relaxation & Rounding

Represent problem as Integer Linear Program(ILP)
Relaxation: relax ILP to LP
Find the optimal fractional solution $x^*$ of LP
- ellipsoid
- interior-point
Rounding: round the solution to a feasible integral solution $\hat x$
Integrality Gap = $\sup_I\frac{\text{OPT}(I)}{\text{OPT}_{\text{LP}}(I)}$

Vertex Cover

Rounding

$$\hat x_v=\begin{cases}1&x_v^*\geq 0.5\newline 0&o.w.\end{cases}$$

Integrality Gap: $2$

MAX-SAT

Random solution

$$P(C_j\text{ is satisfied})\geq(1-2^{-k})y_j^*$$

$\frac{1}{2}$-approximation

LP relaxation and randomized roudning

$$\max \sum_{j=1}^my_j\newline s.t. \sum_{i\in S_j^+}x_i+\sum_{i\in S_j^-}(1-x_i)\geq y_j\newline x_i\in{0,1},y_j\in{0,1}$$

Random Rounding

$$\hat x_i=\begin{cases}1& w.p.\ x_i^\newline 0& w.p.\ 1-x_i^\end{cases}$$

Analysis

$$P(C_j\text{ is satisfied})\geq(1-(1-\frac{1}{k})^k)y_j^\geq(1-\frac{1}{e})y_j^\newline E[\text{# of satisfied clauses}]\geq(1-\frac{1}{e})\text{OPT}$$

$(1-\frac{1}{e})$-approximation

Combination

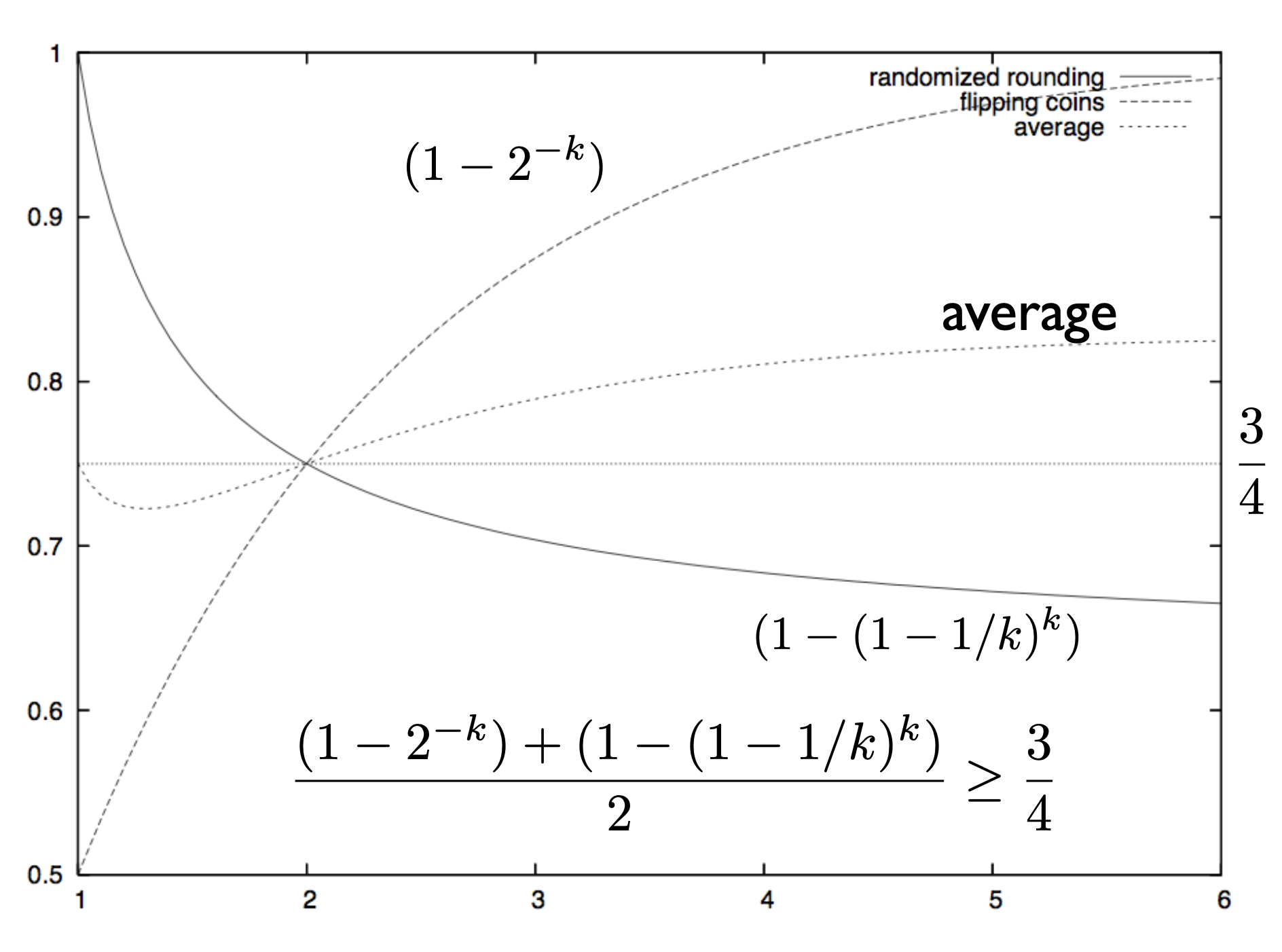
average

Sample random solution, satisfy $m_1$ clauses
Randomized rounding LP-relaxation, satisfy $m_2$ clauses

$$E[\max(m_1,m_2)]\geq E[\frac{m_1+m_2}{2}]\geq\frac{3}{4}\text{OPT}$$

Integrality gap: $\frac{3}{4}$
MAX-3SAT has a $\frac{7}{8}$-approximation algorithm by semidefinite programming and cannot have $>\frac{7}{8}$-approx unless NP=P